Teaching Math in The Next Life

A public lecture performance

University of Western Sydney Abend Seminar

30 July 2020

Arun Ram
School of Mathematics and Statistics
University of Melbourne
Parkville, VIC 3010 Australia
aram@unimelb.edu.au

For many years I’ve been thinking about how to teach mathematics with honesty and inspiration. This has resulted in ideas like “Reality teaching", “Proof machine”, “Marking apocalypse”, and “Just do it”. And then a virus came, and the new life began, online, on Zoom. This will be a talk about the adventures of the past life and the preparations for the next.

INTRODUCTION

First, A special thank you to Roozbeh Hazrat and the other organizers of the Western Sydney University Abend Seminars https://researchseminars.org/seminar/CRMDS for inviting me to give this lecture. I’ve been wanting to organise some material on teaching for a while now, and preparing this lecture finally provided the motivation to do that properly. In the end there’s quite a lot of stuff in this lecture that we’ll only get to taste; I will put the slides up on my website and I do hope that you might enjoy going and following the links and listening to some of the music in full. With that let me begin with my Inbox.

THE NEXT LIFE

A few weeks ago I received a message from a student with the subject line:

Follow up from last Zoom

8 months ago I would’ve had Human Resources knocking on my door asking what kind of substances I was sharing with students.
Instead I got a note from Chancellery thanking me for for doing my best to provide an engaging and supportive environment.

If this isn’t "The Next Life" then what is?

GIVING LECTURE TODAY

This is a lecture about teaching   . . . watch

Sondheim is an inspiring teacher, and I'm sure that some of you know what it feels like to walk into a large lecture theater on the first day of semester with 200 calculus students sitting there waiting for you enter.

Stephen Sondheim

Lyrics modified by Arun Ram

Bless this day
pinnacle of life
student finding classroom
the heart leaps up to behold
this golden day

Today is for Uni
Uni I give you the hope of my future
To raise and lift me
to the top of my greatness
today is for Uni, my hopefully free-and-easy ride

Pardon me, is everybody here?
Because if everybody’s here
I’d like to thank you all
For coming to the class.
I’d appreciate you going even more.
I mean you must have lots of better things to do
You won’t learn a thing from me.
The idiot me. You know, they want me to teach you
But I wouldn’t, I wouldn’t trust myself with anyone
as wonderful as you.
Thank you all, for thinking I was smart,
Thank you all, now it’s back to my office
Don’t get annoyed, but I must disappear today

Bless this day
tragedy of life
lecturer seeing students
his heart sinks down
and feels dread
This frightful day


Listen everybody, look, I don’t know what you’re waiting for
a class.  What’s a class?  
It’s a prehistoric ritual
where everybody thinks I’m qualified,
which is maybe the wishful thought I ever heard,
and it comes with a lecture hall, where suddenly I realise
I’ve got a hundred futures that are my responsibility.

Thanks a bunch, but I’m not going to teach them,
Go have lunch, 'cause I'm not going to teach you,
You've been grand, but I’m not going to teach you
Don't just sit there, I’m not going to teach you
don’t get annoyed, but I must disappear today

Go! Can't you go?
Why is nobody listening?
Goodbye! Go and try
At another person's class.
If you're quick, for a kick
You could pick up a TED talk
But please, on my knees,
There’s a human life at stake!

Listen everybody, I'm afraid you didn't hear
Or do you want to see a crazy man fall apart in front of you?
It isn't only you who would be ruining your life
You know, we'll all of us be losing it
I telephoned my analyst about it, and he said to see him Monday
But by Monday I'll be floating in the harbour underneath the bridge.

I'm not well, so I'm social distancing
You've been swell, but I'm not going to teach you
Clear the hall, 'cause I'm not going to teach you
Thank you all, but I'm not going to teach you
don’t get annoyed, but I must disappear today

Bless this lecturer
totally freaked
slipping under strain
and bless this day
in our hearts
as he starts to explain.

Go! Can't you go?
Look, you know, I really like you all
But why, watch me fry
Like Richmond over Western Sydney?
Look, perhaps I'll collapse
In the abs right before you all
So take back the chalk
Burn the notes, 
and shred the tests.


Look, I didn't want to have to tell you,
But I may be coming down with Covid, and I’m sure I can’t breathe
So if you want to watch me faint, I'll do it happily
But wouldn't it be funnier to go and watch a protest?

So thank you for the twenty-seven emails
Thirty-seven pencils,
Forty-seven videos,
Fifty-seven Calcbooks,
I can’t think to teach you.
I don’t know what to teach you
Please I can’t really help you
I'm not going to teach them
don’t get annoyed, but I must disappear today

REALITY TEACHING

MATHEMATICS EDUCATION

So I really want to be a good math teacher. So I used my resources, and looked up, what makes a good math teacher?

From Wikipedia:

https://en.wikipedia.org/wiki/Common_Core_State_Standards_Initiative#Mathematical_practice

The Standards mandate that eight principles of mathematical practice be taught:

  1. Make sense of problems and persevere in solving them.
  2. Reason abstractly and quantitatively.
  3. Construct viable arguments and critique the reasoning of others.
  4. Model with mathematics.
  5. Use appropriate tools strategically.
  6. Attend to precision.
  7. Look for and make use of structure.
  8. Look for and express regularity in repeated reasoning.

Wouldn't it be Loverly

HepburnLoverlyYouTube

Wouldn't it be Loverly? But, after a few years experience, you become painfully aware that this doesn't quite match reality.

This is some writing on the topic that I did in 2006. It was advice to the new lecturers and tutors for first year Calculus at University of Wisconsin-Madison.

Advice for Lecturers and tutors for first year Calculus at University of Wisconsin.

"It's easier if you mentally try to put yourself in their shoes.

What is the state of a student in your class on the first day?

Last weekend they moved into their dorm room.
This is a totally new experience:
they are leaving family, friends, home, security
and going off to a total unknown where they are going to

get eaten alive by ugly mean professors and TAs

and where they are going to be surrounded by 40000 other students that they have to impress.
They tried to move into their dorm room,
they are tired of moving boxes,
rearranging,
realizing that they forgot their favourite stuffed bunny rabbit that has slept with them since they were 5 years old
(actually, they didn't forget him
but they don't want their roommate to think that they have to sleep with a stuffed animal).

Life is horrible, everything sucks, ...

and then the parties start. 😃

Mifflin Street Block Party

They have met 10000 new people in the last 48 hours,
already gone to quite a few too many parties,
and have walked up and down State Street 4000 times.


The alarm rings on Tuesday morning and gets turned off.
When they finally wake up they have 15 minutes to take a shower
and look smashing before class starts,
they have no idea where Van Vleck is and even less idea what B207 means.



VanVleckB207search



They finally find the room 10 minutes after section starts
and are trying to get oriented as to what the heck is going on in your class in the first few seconds when they walk in.
Perhaps, the worst thing you can do is add to their insecurity by getting on their case for being late to your section.

Your job is to get them started, on track,
oriented to the course and focused on mathematics.

Your job is to teach them calculus.

How to connect Math Education and Reality Teaching?

Well, that is the goal, every time we enter that Zoom room.

ENGAGEMENT WITH THE STUDENTS

And so, of course
we must do our best to engage with these Reality students
To make the mathematics so active
that they forget about the parties that they went to yesterday
and start thinking about Calculus.

ACTIVE VERSUS PASSIVE

My new home rigged document camera!

DocCamera

My new chalkboard!

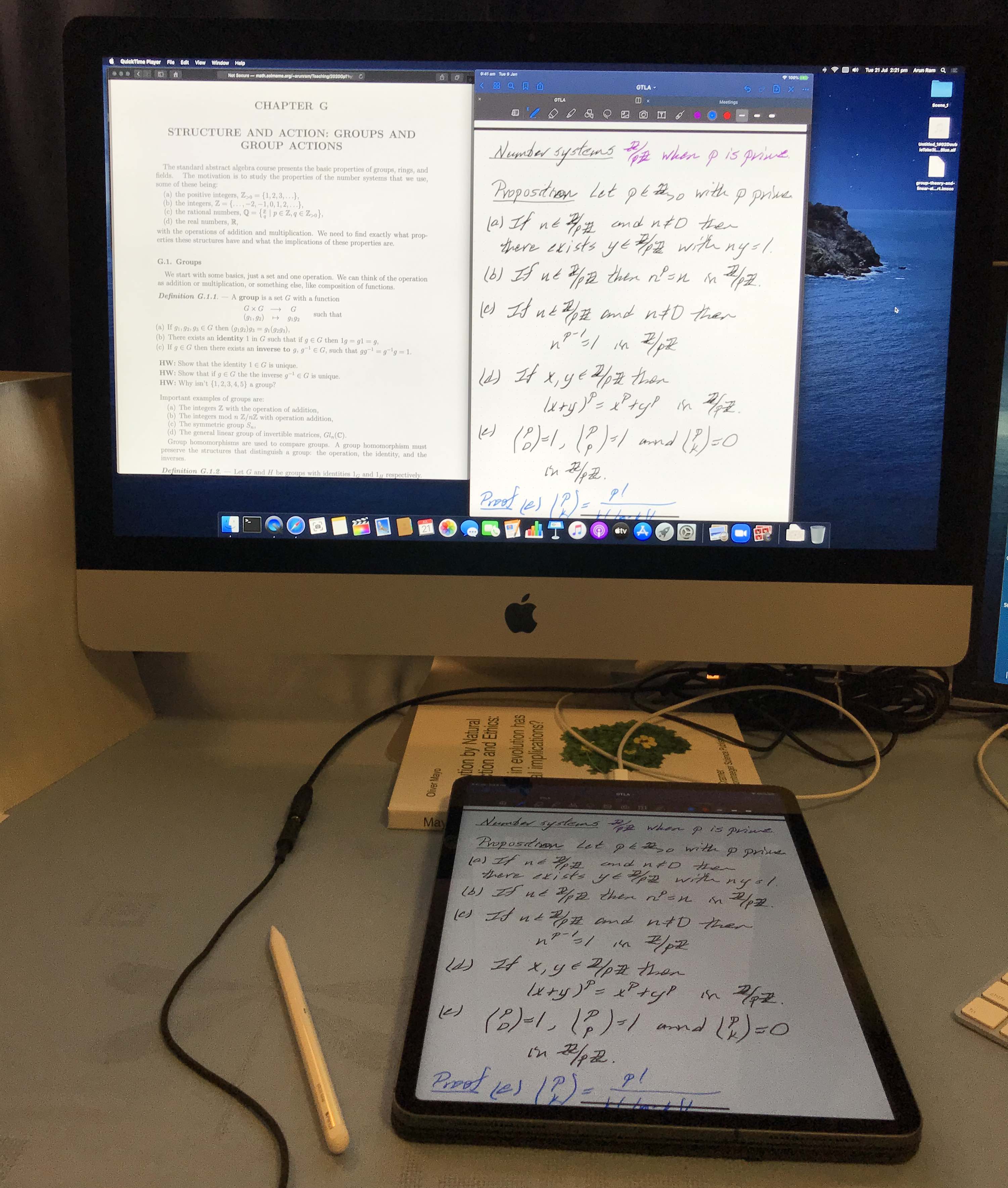
Chalkboard

What are you paying us for?

There are SO many resources available from Google that there is NO WAY that you can NOT learn math.

https://math.stackexchange.com/questions/2792100/the-integral-of-sin-x-2

You could do it all yourself, with the resources that are just out there, available to everyone.

https://www.khanacademy.org/

What we are providing for you, is real help managing your time --
We are helping you not procrastinate it all away.
We are providing you with assignments and exams with due dates and marking them to give you motivation to do them.
And you pay us for it.
For good reason, because it’s hard work to get you off your bum and working and doing productive learning.

One of the blurbs on my web page is:

Teaching, for me, is a consuming activity. I enjoy it immensely because it is an act of human communication, and I also get pleasure from the exercise of organizing material into "nice packages". Teaching requires serious thought and effort because it is an attempt to help someone else learn. Even for oneself, learning takes discipline and focus, and getting someone else to learn is a challenge.

In fact, if you really think about how hard that is, you should probably be paying us more than you do. 😎

Procrastination, that's the challenge here

But you know what? Your mates, and your mentors, can help you too. They REALLY can help you.

Ever been at a creche and there is some kid that has to go wee and is avoiding it?
And you can tell they're avoiding it.
You, as a mentor, as a teacher, as a friend, as a best mate, can help them.
You tell'im,

Billy go use the toilet,
and then you can come back and play more space monsters.
We’ll wait for you and have some fudge brownies after you get back.
And you watch Billy’s face,
he turns to tell you no,
and then,
in a split second he thinks about that fudge brownie and how he actually does need to wee pretty badly,
and off he goes …

Think about it, It’s lots easier to get up and go for an early morning run if you have to meet someone.

Get your mates, together, do that assignment, and NOONE is allowed to have a drink until everyone gets their assignment done. You’ll be amazed at how well this works to have everyone get it done faster than they ever have before. And how much better that drink and that snack tastes after the assignment is done.

This is my favourite example of how mates really work together to achieve excellence,

a performance art,           a study of beauty,           a perfection of communication,           mathematics.

BTS Dance Assignment 3 -- worth 64%

MARKING APOCALYPSE

All math teachers must teach their students forcefully that doing mathematics is

a performance art,           a study of beauty,           a perfection of communication,           mathematics.
Instead students are sometimes taught (probably unintentionally) to focus on
getting the right answer
instead of focusing on the
justification and communication of the amazing reasons leading to conclusions.
Indeed, most frequently,
the complaints I hear most often from university lecturers about teaching students at the tertiary level,
are that the students are not interested in understanding and explaining why the mathematics works, only in the precooked answer.
And the students are convinced that this is the way that mathematics is done,
even though,
I, as a professional mathematician, know that that is not right.

I thought about this,
but I couldn't convince myself that math teachers in primary school and high school were actually trying to teach their students that there are no good reasons behind the beautiful mathematics. At first I thought it must be because our primary and secondary math teachers don't know any other way.

But then I went to go visit an old friend of mine from my teenage years, who has now become a high school maths teacher. She first became a radiologist, but after her kids were born, she wanted to spend time with them, so she quit the intense world of clinical radiology. Then, after her kids went to school, she wanted to do something important for the world and the future generation and so she became a high school math teacher.

My friend is very very smart, and I knew that she knew her mathematics, and that she certainly would have her intentions and knowledge focused towards the best possible for the mathematics and for the students.

She explained to me.

The students learn (from repeated experience via worksheets that are designed to reduce grading time) that
Did I get the right answer? Yes
should result in full marks for the problem.

The reason that this viewpoint is so frequently promoted by teachers is
a desperate survival method from teachers that need to save on grading time.
Formats for worksheets, particularly those that leave some space between questions but which do not leave sufficient space for working the problem, perhaps only enough room for entering an answer) have the (perhaps unintended) consequence of teaching the student to focus on the answer and not the communication of mathematics and the argument justifying the conclusion.

The lack of time for grading, is the major factor in encouraging these habits in teachers and their students. Just do the computation. If you are a high school teacher, and you teach 4 periods per day, with 20 students each, and you have them do a worksheet each day (which they probably should do, to develop their skills) then, at the end of the day, you have to grade 80 worksheets. It takes at least one minute per student just to organise the papers and to carefully record the marks, so, not even having started actually reading what they've written or providing any sort of feedback to the students, that is 80 minutes of work for you to do after teaching four classes and managing 80 students and their subtlties in person earlier in the day. And you still have to prepare for tomorrow's class.

Repeated experience from worksheets designed to reduce grading time,
a desperate survival method from teachers, ...
The marking apocalypse: the students learn to think that only the right answer matters, and that reasoning will not receive credit or attention.

Any solution to the mathematics teaching challenge needs to address the marking apocalyspe.

Things will be better Assignment 4 -- worth 20%

HONESTY

One of the things that is important to me is honesty and directness in my interactions with students. I feel that it is important for me, as a teacher, to be a role model in this respect.

One of the frequent situations that is difficult for me,
is when a student carefully and cautiously comes to my office to ask me something.
Most often they stand at the portal,
not daring to cross it into my office,
and say, tentatively,
"Are you busy?”

Which, of course, is not really what they mean.
What they really mean is
“Will you talk to me right now?”

But the way that they have chosen to put the question,
creates a difficult situation for me.

To be honest, I have to answer
“Yes, of course I’m busy.
If I wasn’t busy I would be sitting here in my office
twiddling my thumbs and staring out the window.
And if I was doing that,
then I wouldn’t be doing my job,
which would mean that I should be fired.
So, by the very fact that I want to keep my job,
and that I would like to do a good job in my job,
because of that,
I am busy.

"But, let me stress,
a major part of my job is to help students as much as I can,
so the question that you didn’t ask, but meant to ask, is
“Will you talk to me right now?”

"And the answer to that question is definitely yes,
I will talk to you right now,
and, not only that,
I view it as a particularly important part of doing my job well,
so please do ask me, now, what you want to ask me."

Then there is a great pause.

There are two kids of students:
the ones that, after this little speech,
ask their question,
and
the ones that feel an uncontrollable effort to be extra polite and ask me,
“Um, ..., are you busy?”

I notice, how much pressure there is,
built into the mechanisms of our society,
pushing me to be dishonest.
I must admit that, very often,
I just give in and lie:
so that when a student asks me
“Are you busy?”
I just respond,
“No, how can I help?”

But every time I do that I know that I am being dishonest
and that I am subtly teaching that student that it is acceptable to be dishonest.
But I’m not completely sure that I should do that.
Where should we draw the line in the level of dishonesty in our responses?

Honesty Assignment 5 -- worth ∞%

Parking Completo album cover

PLAGIARISM

Speaking of honesty, one of the things we have our students do at University of Melbourne, for every assignment submission, is sign a "plagiarism declaration", which is some kind of honour code saying they won’t plagiarise.

I asked the students what it meant. They told me they are not supposed to work with any else on their work for this class. I told them no, that’s not what it means, that’s completely crazy, and that is not good problem solving technique.

Good problem solving means using your resources, and, most of the time, your best resources are other people. Being a good scientist means solving problems by using your resources, not by reinventing the wheel. If we, as scientists, worked by reinventing the wheel every time, we would not have iPhones or credit cards or vaccines. Because we would still be trying to figure out how make and control fire. And each individual scientist would be in their own individual cave trying to do it by themselves — nobody working together. A perfect recipe for NOT making progress.

Not plagiarising means acknowledging (loudly and clearly and thoroughly) your sources and your resources. That means, if Jean-Pierre Serre taught you how to solve this problem, you be a good scientist and acknowledge that in your solutions to question 3 on the assignment, and give a proper, complete, reference.

Somehow the students have gotten a completely wrong idea about this plagiarism thing. We should tel students that it is

a good thing to use StackExchange,

(that there are, almost certainly, better resources for the task), and that

THEY MUST REFERENCE PROPERLY

(in all cases and also when they use StackExchange) and

IF THEY DON'T THEN THEY ARE BAD SCHOLARS

and they have lost all respect I might have had for them.

And that goes for lecturers and professors too — put in proper referencing:

I learned this from the 3rd paragraph of the unpublished letter of Pierre Deligne,
which is now available on the internet at
https://mathproblemsolutionsforfree.com/Delignes-letter-where-he-says-how-to-prove-the-Riemann-hypothesis
If you don’t do proper referencing, then you are not being a good scientist, and you are plagiarising.

If you do proper referencing, then however you solved the problem, you are not plagiarising.

Queen of the Night Aria Assignment 4 -- worth -∞%   i.e. end of career

MARKSISM

My students say I’m a MARKSist

They don't mean Marx and Engels.

Marx and Engels

Marks and Engels

They mean marks and angles.

marks and angles

My students say I’m a MARKSist

This is their way of saying that quality writing is important to me — quality mathematical writing.

Quality Mathematical Writing

This is how we work on it together.

When taking an exam, what is the goal?

NOT to finish,
NOT to do all the questions,
NOT to answer everything in gory detail.

The goal is to optimize your marks.

For each question you want to get "the bulk" of the marks, not "all the marks".

Only if you have extra time after getting "the bulk" of the marks in place,
then (and only then) should you go back and tighten up to try to get close to "all the marks" on some questions.

There's nothing more painful for a marker than seeing a student do really well on question 1 and then seeing that their successive questions get more and more frantic and incomplete. You know they wasted too much time on question 1 and didn't properly do the other questions. You know that they didn't do the exam in a way that optimised their marks. And, its painful to see that. But there is nothing that you, as a marker, after the fact, can do, when a student chooses to take an exam and not optimise their marks. It was their choice not to learn how to optimise their marks.

And so,
in class, we ALWAYS talk about marking.
For every example that is done in class, we talk about

which parts of the solution     (the key step, for example)
receive more marks than other parts (a sign error, or an arithmetic error, for example).

We discuss,
how to communicate with the marker in what you write:

I know I shouldn't be getting a negative answer for the volume of a sphere, but I can't find the sign error in what I did above.
and how that little sentence demonstrates understanding, puts the marker on your side and optimises the marks you receive.

We talk about how
markers can't read minds and get confused,
and that is why
solutions that are in a haphazard order, or
without equal signs where they should be, or
aren't written well,
receive fewer marks.

We discuss all of these things, every class, over and over. It is a way to teach

QUALITY MATHEMATICAL WRITING             and             COMMUNICATION SKILLS

and

TO OPTIMISE YOUR MARKS ON THE EXAM.

It is a skill, and you learn it like any other skill, just like learning to drive or to write or to work your iPhone.

I’m definitely a MARKSist.

Quality mathematical writing Assignment 4 -- worth 91%

PROOF MACHINE

An important component of quality mathematical writing, is being able to write proofs that are correct, complete, and

easy for the reader to read and understand.

As a teenager I hated writing. And when it got to proofs, I just couldn't figure out how people did it. And when I started reading math papers, Oh-My-Goodness, reading other people's proofs is often REALLY HARD (although I did notice that there are a few authors, like Macdonald and Deligne, where I find the proofs consistently easier to read).

Ian Macdonald      
Pierre Deligne
Pierre Deligne
Ian G. Macdonald

In was in my first year or two as a postdoc at University of Wisconsin that I got assigned to teach the undergraduate Abstract Algebra course and so I needed to figure out how to explain to my students how to do the necessary proofs. That was the catalyst for me to formulate the mechanism that I now call “proof machine”.

  1. There are very few words needed in the structure of a proof. Organized in rows by synonyms they are:
    2.  
    To show
    Assume, Let, Suppose, Define, If
    Since, Because, By
    Then, Thus, So
    There exists, There is
    Recall, We know, But
     
  2. The overall structure of a proof is a block structure like an outline.
    3.  
    To show: If   A   then   B   and   C  .
    Assume:   A  .
    To show:
    (a)   B  .
    (b)   C  .
    (a) To show:   B  .
                   .
                   .
                   .
         Thus   B  .
    (b) To show:   C  .
                   .
                   .
                   .
         Thus   C  .
    So   B   and   C  .
    So, if   A   then   B   and   C  .
     

    Here is an example:

    Let f:S→T be a function. An inverse function to f exists if and only if f is bijective.

    Proof.
    1. ⇒ Assume f:S→T has an inverse function f-1:T→S.
    2. ⇒ To show: (a) f is injective.
    3. ⇒ To show: (b) f is surjective.
    4. ⇒ (a) Assume f(s1) =f(s2).
    5. ⇒ (a) To show: s1=s2.
      6. s1 = f-1 (f(s1)) = f-1 (f(s2)) = s2.
    6. ⇒ So f is injective.
    7. ⇒ (b) Let t∈T.
    8. ⇒ (b) To show: There exists s∈S such that f(s)=t.
    9. ⇒ (b) Let s=f-1(t).
    10. ⇒ (b) Then
      11. f(s) =f(f-1(t) )=t.
    11. ⇒ So f is surjective.
    12. So f is bijective.
    13. ⇐ Assume f:S→T is bijective.
    14. ⇐ To show: f has an inverse function.
    15. ⇐ We need to define a function φ:T→S.
    16. ⇐ Let t∈T.
    17. ⇒ Since f is surjective there exists s∈S such that f(s)=t.
    18. ⇐ Define φ(t)=s.
    19. ⇐ To show: (a) φ is well defined.
    20. ⇐ To show: (b) φ is an inverse function to f.
    21. ⇐ (a) To show: (aa) If t∈T then φ(t)∈S.
    22. ⇐ (a) To show: (ab) If t1,t2∈T and t1=t2 then φ(t1) =φ(t2) .
    23. ⇐ (a) (aa) This follows from the definition of φ.
    24. ⇐ (a) (ab) Assume t1,t2∈T and t1=t2.
    25. ⇐ (a) (ab) Let s1,s2 ∈S such that f(s1) =t1 and f(s2)=t2.
    26. ⇐ (a) (ab) Since t1=t2, f(s1) =f(s2).
    27. ⇐ (a) (ab) Since f is injective this implies that s1= s2.
    28. ⇐ (a) So φ(t1) =s1=s2 =φ(t2).
    29. ⇐ So φ is well defined.
    30. ⇐ (b) To show: (ba) If s∈S then φ (f(s))=s.
    31. ⇐ (b) To show: (bb) If t∈T then f( φ(t))=t.
    32. ⇐ (b) (ba) This follows from the definition of φ.
    33. ⇐ (b) (bb) Assume t∈T.
    34. ⇐ (b) (bb) Let s∈S be such that f(s) =t.
    35. ⇐ (b) (bb) Then
      36. f(φ(t)) =f(s)=t.
    36. ⇐ (b) So φ∘f and f∘φ are the identity functions on S and T, respectively.
      37. So φ is an inverse function to f.
    □

  3. Any proof or section of proof begins with one of the following:
     
    (a) To show: If   A   then   B  .
    (b) To show: There exists   C   such that   D  .
    (c) To show:   E  .
     
  4. Immediately following this, the next step is
     
    Case (a) Assume the ifs and 'to show' the thens. The next lines usually are
    • Assume   A  .
    • To show:   B  .
     
    Case (b) To show an object exists you must find it. The next lines usually are
    • Define   C=xxx  .
    • To show:   C   satisfies   D  .
     
    Case (c) Rewrite the statement in   E   by using a definition. The next line is usually
    • To show   E'  .

DON'T think. That just confuses me. Following the method almost always produces a proof without thinking. Most of doing proofs is simply rewriting what has come just before in a different form by plugging in a definition.

The most important factor in learning to do proofs is practice, the same as anytime that one is learning a new language.

MEMORIES

It was in the second semester of my undergraduate education at MIT that I first met pure mathematics, open and closed sets, the book “Baby Rudin”, and Warren Ambrose.

Baby Rudin      
Warren Ambrose
Warren Ambrose
 
A tribute to Warren Ambrose, by I.M. Singer and H. Wu,
Notices of the American Mathematical Society, April 1996.
http://www.ams.org/notices/199604/comm-ambrose.pdf
Baby Rudin

The course was ‘18.100 Mathematical Analysis’. Warren Ambrose had a great effect on me. Somehow we had a one-to-one conversation where we both confessed that our true love was music and that we were doing math only as a backup. At the time, I was still far from being a professional mathematician and he was a famous geometer nearing the end of his career and his life (it was 1984 and he died in 1995 at the age of 81). He told me that he had been a jazz trumpet player but an accident had made him unable to play properly and so he had pursued mathematics for a profession. His exams (two midterm exams and a final) were all 24 hour open-book closed-friend take-home tests: 10 questions, true or false, graded 1 if correct, -1 if incorrect, and 0 if not answered. The average score across the class (about 20 students) was often around 0. But this mechanism taught you better than any other what proof meant – if you were unable to provide a proof you believed in then you risked getting -1 for that question. The questions were always very interesting. I carried those questions around for years until sometime in 2012 when I accidentally left them in a classroom and, when I came back to find them an hour later, they were gone.

Prayer -- marks allocated 0

Prayer

CURRICULUM AND ASSESSMENT

TEACHING LARGE CALCULUS CLASSES

The first time I really rewrote a course was in 1999. It was the first time I felt that I could take full responsibility and I took the opportunity to try to implement several features that I had been thinking about for effectively teaching large calculus classes in large US State Universities.

Large calculus classes was a framework I was very familiar with.

I first experienced such calculus classes as a student at New Mexico State University in 1982.
We used Thomas and Finnney 5th Ed.

ThomasFinney5thed

When I went to India in 1983, right after graduating from high school, my father and I went to Karol Bagh, to where all the technical book shops are and I picked up the standard Indian calculus books, which are very much geared towards the All India Secondary school exams. They have a little bit of text, and then lots of examples of questions from past All India exams.

AggarwalSeniorSecondaryMath

I took calculus again as a student at MIT in 1983. We used Thomas and Finney 5th ed.

ThomasFinney5thed

Then in 1985 I started as a TA teaching discussion sections. We used Thomas and Finney 5th ed.

ThomasFinney5thed

I continued as a teaching assistant throughout graduate school until 1991. We used Thomas and Finney 5th edition.

ThomasFinney5thed

Then I went to University of Wisconsin and experienced the large calculus classes there in 1993 and 1994. We used Simmons, which, as far as I can tell is homeomorphic to Thomas and Finney 5th edition.

SimmonsCalculus   ≃ ThomasFinney5thed

In my 6 years as a teaching assistant, I observed that the students needed to learn how to do the problems on the exam. It was the same when I was a student and it is the same now. And the Indian books had great lists of problems, and doing problems on those lists was what eventually made me pretty good at Calculus.

ASSESSMENT

After a few years of teaching you quickly learn where the pain points are as a lecturer. Making exams is always onerous. You try to think up good questions. Too often you enter an infinite loop trying to tweak them so that the numbers and the equations aren't too messy. And then you have to balance out the exam. And then make sure it’s not too long.

And you’ve been working on this annoying task for many hours over several days, and the students start badgering you with questions about what kinds of things will be on the exam. And you end up squirming, trying not to give it away, and to stay pleasant and not get snappy with them and their incessant pushing.

I soon began to realise that I had to find a better way.

I started to think about this whole exam thing.
Maybe we could do without?
Where did all this exam framework come from?
What is good about it?

After some thinking I realised that the exam framework has a huge, very powerful, psychological effect on the student. It is the only thing that makes them study the subject at all — At least that's the way it was for me as a student. I had so many parties to go to, so many movies to see, so many important nights out with friends, that I certainly wasn’t going to think about calculus at all unless I had an assignment to turn in, or an exam coming up.

So, the whole thing, at least in my case, was really a psychological trick to manipulate me into doing the work to learn the material.

I began to study the assessment question -- to watch how people do assessment in real life.
I mean, in real life, in every human interaction, you are assessing me and I am assessing you.

How much Shakespeare do you know?

How much French can you speak?

Is your knowledge of history up to snuff?

Do you know what Kanye West said to Kim last week?

I’m checking you out, you are under assessment.
It's a real life exam.

WELCOME TO CANADA

It crystallized for me, how we do it, one time when I was traveling to Canada. It was pretty early in my research career, I had been invited to give a research lecture in Montreal, and I was quite proud. It was, for me, one of the first times that my trip was being paid for by the host institution, and I had been invited to give a talk. I felt that I was just starting to make it in my “business”, which was mathematics research.

On the plane, the fight attendants handed out arrival cards for arrival into Canada, where we would have to pass through immigration. For the first time, I was able to tick the box that I was traveling on “business”, and I did so with pride.

I very quickly learned not to do that.

When I got up to the front of the line,
the officer looked at my form and said,
"You’re traveling on business?”
“What kind of business do you do?”
I responded proudly: “I’m a mathematician”.
No response.
He wrote something on the corner of my form and told me to go sit over on one of those chairs over there and wait for the agent.

(This was not looking good).

After waiting 10 minutes or so,
watching all the others on the flight pass on through immigration and head off to collect their bags,
the agent came out and got me and took me over to a separate room for a “little interview”.
She was very pleasant, but she had a formal border patrol uniform and a look like she could to turn into a very tough woman when necessary.

She asked what I was going to be doing in Canada and how long I was staying.

I told her that I was there for 3 days on a visit to the mathematics department at University of Quebec at Montreal and that I had been invited to give a talk in their research seminar.
She said,
“I see, that’s your business?”
“Yes, I said, "I’m a mathematician”.
She asked me what my home university was.
I told her, “I’m an assistant professor at Princeton University”.
She said,
“So you’re a mathematician, are you? What’s the integral of x3?”

A bit taken by surprise, I responded

14x4, plus any constant if you want to be thorough”.

She said, “Welcome to Canada.” and waved me to the door.

The integral of x3 Assignment 4 worth 15%

EXAM DESIGN

At that moment it hit me how we actually do assessment in real life. We ask a random question, usually a fairly easy one, but random, from some huge list for that subject “in the cloud”. And if the responder can answer immediately and correctly, they pass, and if not they will be interrogated further and in much greater detail.

That was when I formulated my method of exam design.

I make a list of all questions, ALL questions, that could appear on the exam. I do this by taking all the textbooks relevant to that course off my bookshelf and copying out all the problems in them. Then I make that list public, and tell the students, on day one of the course, that these are the problems that might appear on the exam.

To make the exam, I use the computer to generate random numbers.

RandomNumbers

Then I, myself, start doing the questions that the computer has listed for me. I write my answers in the same way that I'd like the students to be writing their answers -- easy to grade, covering the most important key points properly.

After 1 hour, I stop. That is a 3 hour exam for the students. I has taken me 1 hour and ten minutes to prepare, and I have already made the solutions to give to the graders.

I have been amazed at how well this works. These are positives:

  1. I can honestly tell the students,
    there is no problem on the exam that they haven’t seen before.
    The list is 100 problems per week of teaching,
    so for a 12 week course it is 1200 questions.

  2. The goal is clear,
    they have to learn how to do these questions.
    And my job as a teacher is to help them learn how to do these questions,
    in whatever the best way that I can is.

  3. During the semester I have no hesitation about doing any problem for them --
    Showing them, in detail, how to write the solution well in order to maximise their marks.
    There are plenty of others on the list to be done,
    and their job is to learn the skill of doing these questions and writing the solutions in quality presentation.

  4. I tell the TAs to do any problem that the students ask them to do for them.
    In class, I choose my in-class examples from the list.
    Since those problems are on 'the list', the students are motivated in class to follow and work through the example.

  5. When physicists and engineers and biologists suggest that we are not covering what their students need to learn,
    I invite them to make a list of the problems they want the students to be able to do before they enter their physics/engineering/biology course,
    and I put those questions on 'the list'.

  6. 'The list' provides consistency across streams.
    Every lecturer and tutor can teach in the way that works best for them,
    and, at the same time, everybody is clear, and completely consistent,
    that the assessment will be chosen randomly from the problem lists.

  7. And it removes the terrible pain of trying to design and wrtie new exams.

The students always complain that it is too many problems.
But I explain to them that this is only a psychological thing.
If I want to teach basic multiplication of positive integers,
the number of pairs of positive integers less than 100 is 10000,
and so, just lke that, I have a list of 10000 problems.
No sensible person would memorise solutions to 10000 multiplication questions,
simply because it is so much more efficient to learn how to multiply.

The same mechanics works for the calculus problem lists. There is no point memorising how to do 200 different derivative questions and 200 different integrations, because it is so much more efficient to learn to take a derivative and do an integral. And isn’t that what we want them to learn anyway?

CURRICULUM DESIGN

From my website:

This page is built on the philosophy that the way to specify a curriculum is to specify what kinds of tasks will be expected, i.e. what the assessment will be. In other words, a curriculum is determined, whether we admit it or not, by specifying what questions can appear on the exam. If the students are not expecting a question on the exam, then the likelihood that they will learn to do that question is very low.

THE ULTIMATE HANDBOOK ENTRY

The exam will be 3 hours, chosen randomly from the following list.

Click here for the course problem list

Your goal is to maximise your marks on the exam.
Our goal is to help you learn how to maximise your marks on the exam.

f(x) Assignment 4 worth 25%

Fxthumbnail

Just Do It

A frequent event for me, ...
A student comes to my office and says
"I can't do problem 14 on the problem sheet."

"What's the difficulty?", I ask.
"I'm just completely stuck", replies the student.

"Ok, write the problem on the board, let's look at it".

"It's this one here ..."
and they hold up their problem booklet 5 meters away.

"No", I say, "write it on the board, I can't parse it from a distance.
Write it on the board, and then we can have a look at this equation."

Eventually, they get it written on the board
and then they turn and look at me with this semisad look,
half expectancy, half scepticism,
definitely a look indicating that they feel they deserve my pity
for their terrible predicament.

"Great", I say, "now we know what the question is,"
"Go ahead", "Just do it".

They look at me with shock.

"What do you mean?" they ask.

I mean, "Just do it, start on the left hand side,
let's see what comes out".

"Go ahead, write on the board, the left hand side."

They look at me like I've gone off the deep end.
I look back with my best look of patient expectation.

Finally they write the left hand side on the board.
Then they turn and look at me with this semisad look,
half expectancy, half scepticism,
definitely a look trying to convince me that they deserve my pity
for their terrible predicament.

"Great", I say, "Keep, going, Just do it."
They look at me like I've completely lost it.
"What do you mean?."

"I mean, great, now you've written the left hand side,
now take the derivative just like it says to.
Let's see what comes out".
"Go ahead, write the next step on the board."
I put on my best look of patient expectation again.

They look back at me and respond,
"Well I know that the derivative of sine is cosine,
but then I have no idea where to go from there."

I say, "Neither do I.
I have no magical ability to predict the future.
Just take the derivative of sine and write the next step,
and then we'll see if we can figure out what to do next."

With great reluctancy they write the next step on the board.
Then they turn and look at me with this semisad look,
half expectancy, half scepticism, definitely a look indicating that they feel they deserve my pity
for their terrible predicament.

I say, "Great, now do the next step, go ahead, just do it.
They look at me with wonder.
"You mean multiply out?"
I say, "Yup, that's what it says to do, let's do it.
Write it on the board".

They multiply out.
Then they turn to me and say
"Now I could use the identity sin2 + cos2 = 1 is that ok?"
I say, "I don't know, just do it, let's see what comes out."

They write the next step.
Then they don't even turn to look at me,
they say
"and now I can make a common denominator",
and they write the next step.
They say "Now I'll cancel the 2"s,
"And that gives me x2 -4cos(2x),
is that the answer in the back?"

And they look up the answer in the back.
"Yeah that's it, that's the answer in the back," they say.

I say, "Great,
now where was it that you were totally stuck?"
They respond,
"I don't know, I just had no idea what to do."

So often the easiest and most efficient solution is

JUST DO IT.

In spite of the fact that a very profitable shoe company prints it on all their products,
it's fascinating to observe people,
and the lengths that they will go to,
to convince themselves that it can't be done,
at least not right now,
not at this time of day.

JUST DO IT.

But, if I'm being honest,
I'm like that too. All the time.
It's a form of procrastination.
I dance around avoiding what I should be doing, ...
the calculation that I know I have to do for the next step in my research ...
I find every other thing that needs to be done ...
vacuuming, ...
calling my mother, ...
reading the BBC News, ...
going for a coffee and sitting moping
about how my research isn't going as fast as I would like, ...

It's all a very intricate game I play with myself to procrastinate.
It would be so much easier if I just did for myself what I tell the students:

JUST DO IT.

Itzhak Perlman master class with Cho Liang Lin -- start at 54:32

Engaging students online: The Clock Number System

YouTube video:

I made a little lecture video on the clock number system, and put it on my teaching YouTube Channel. My teaching YouTube channel is called "proof machine".

The Clock number system

Email to students:

The first Number System you learn as a newborn is the clock. Your parents are obsessed with it. They look at a round thing on the wall, say something about adding 1 or 2, and then make a life changing announcement about when you will eat or get a nappy change. They decide how long you will sleep from the clock and when they won’t pay attention to you.

Very soon you learn that if you go down for a nap at 12 and sleep for 2 hours then you wake up at 2, just in time to change a nappy and go for a ride in the pram around the park. That’s how you learn that 12+2 = 2.

Very soon you learn that there is a nappy change every 3 hours and that there are 4 nappy changes during the day and 4 nappy changes at night. That’s how you learn that 3x4 = 12.

Professional mathematicians call 12 zero because 12+2 = 2, and even though you know, since birth, that 3x4=0, primary school teachers get all upset when you point out that two nonzero numbers can multiply together to give 0.

In the clock number system, what is the prime factorization of 6?

PS In the French language the word for clock is montre. In mathematics language the word for clock is Z/12Z (zed mod 12 zed).

After a couple of tests with students, the evidence is that, in this case, the email is actually more effective for engaging the students with this topic.

Engaging myself, as a teacher, with an old topic

Let's be honest, one of the challenges as a teacher, is keeping oneself engaged. I have taught Calculus about 30 times over the last 30 years. I have to make sure that I am not bored with the subject and unintentionally transmitting that boredom to the students.

I find that if I actually sit down and really think about the subject each time, and figure out a way to say it better than I did in previous years (the records of how I said in many previous years are available from my web page) then I always learn something new and interesting.

This year I discovered a formula I had never seen before!

I was thinking about What makes a derivative?

Well we have the addition property:

d dx ( f+g) = df dx + dg dx

We have the multiplication property:

d dx ( fg) = f dg dx + df dx g

And then I started to think about, ... what else do we really need? I mean, for the students to do the problems on the exam.

They don't really need any quotient property because you can always derive it from the multiplication property,

d dx ( fg ) = d dx ( fg-1 ) provided we know how to do d dx ( g-1 )

So what we really need is a power property. That's the other construct we seem to have in so many expressions: ab. So I worked it out. This is what I got.

d dx ( fg ) = fg ( gf df dx + logf dg dx )

I was shocked. I had never seen this formula before!
I pulled all the calculus textbooks off my shelf and searched for it.
Nope. I found this one:

d dx ( xc ) = cxc-1

which, is a consequence of my power property since d dx ( xc ) = xc ( cx dx dx + logx dc dx ) = xc ( cx ⋅1 + logx ⋅0 ) = cxc-1

I found this one,

d dx ( ex ) = ex
which, also is a consequence of my power property since d dx ( ex ) = ex ( xe de dx + loge dx dx ) = ex ( xe ⋅0 + 1⋅ 1 ) = ex

Then, I realised that, with my power property I could directly do "really hard" questions like

d dx ( xx ) and d dx ( (sinx) cosx )

So,

NOW I HAVE THE POWER             d dx ( fg ) = fg ( gf df dx + logf dg dx )
Watch out, here I come.
May the FORCE be with you.

The FORCE Assignment 7 -- worth 1000000000%

Thank you.

Arun Ram
School of Mathematics and Statistics
University of Melbourne
Parkville, VIC 3010 Australia
aram@unimelb.edu.au

The images are from the following sources: