Buildings
Last updates: 11 August 2012
The concept
A building is an axiomatization of the flag variety of a Kac-Moody group . The advantages of the building point of view are
- a "conceptual picture" of the geometry of the flag variety
- a good view of the "independence" of the geometry from the underlying field,
- a powerful way to work with tori by viewing them as apartments.
The disadvantage is that the axioms do not allow for certain spaces that ought to be considered as flag varieties of "Lie type" groups and this dichotomy between buildings and Lie type groups is unhealthy.
Let be a group, a subgroup of and let be an index set for the double cosets of in so that
Morally, the building of is the set with the function given by In the case when is a Borel subgroup of a reductive algebraic group then is a group with a distinguished set of generators: a Coxeter group. The usual approach to buildings is to axiomatize building in terms of the group and its special choice of generators.
The definition of a building
A chamber system , or flag system on a set is indexed by the elements of . The set is the set of chambers or flags and the relations are the adjacency relations. For a fixed chamber , the chambers -adjacent to look like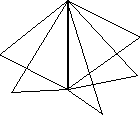 When
is the same for all and ,
A gallery of type
is a sequence
A Coxeter group is a group
with a given presentation by generators , and relations
where
is the order of
( is allowed). Hence, the data of a Coxeter
group is the set
A building of type is a chamber system
over with a function
such that
When
is the same for all and ,
A gallery of type
is a sequence
A Coxeter group is a group
with a given presentation by generators , and relations
where
is the order of
( is allowed). Hence, the data of a Coxeter
group is the set
A building of type is a chamber system
over with a function
such that
- If and then there exists with .
- If is a reduced expression and there is a gallery of type from to then .
A geometric realization of is a realization of the simplicial complex which has
- vertices: ,
- simplices: ,
Apartments and retraction
Let be a Coxeter group. The Coxeter complex of is the building given by A geometric realization of is the reflection representation of where the chambers are the fundamental regions for the action of .
Let be a building of type . An apartment is a sub-chamber system of isomorphic to the Coxeter complex .
- If then there exists an apartment such that .
- If are apartments such that then there is an isomorphism such that .
- Apartments are convex: If a chamber lies on a minimal length gallery joining chambers and then lies in every apartment containing and .
Reformulating the axioms of a building in terms of apartment, a building of type is a simplicial complex with a collection of subcomplexes, the apartments of , such that
- ,
- If then ,
- If then there exists such that and ,
- If and then there exists an isomorphism such that .
Let be an apartment and a chamber in . The retraction onto centered at is the map where is an apartment containing both and and is an isomorphism.
Affine buildings
Let be an affine building. An alcove is dominant if it is on the positive side of for all . The dominant chamber is A sector is a subchamber system of isomorphic to .
- If is a sector and is a chamber in then there exists an apartment containing and a subsector of .
- If and are sectors, then there exist subsectors and which lie in a common apartment.
Let be an apartment and a sector in . The retraction onto centered at is the map where is an apartment containing and a subsector of and is an isomorphism.
The spherical building at infinity or boundary of is the set of equivalence classes of sectors with respect to the equivalence relation where and are parallel contains a sector.
Dictionary to algebraic groups
Let be a linear algebraic group. Let be the Weyl group and let be a Borel subgroup of . The is a (spherical) building of type such that so that Let be the group over the field , the affine Weyl group, and let be an Iwahori subgroup of . The is an (affine) building of type with In our favourite chamber, vertex, apartment and sector are respectively. If is the favourite sector, its equivalence class has stabiliser and is a bijection between the building and .
Let . Then
On the classification
Most buildings are constructed as in (???) and (???). There are only a few "exotic cases" when the rank is 2 or 3. The classification of spherical buildings of rank ≥ 3 [?] and of affine buildings of rank ≥ 4 [Tits, Como] says that they are the buildings corresponding to BN-pairs in untwisted or twisted Chevalley groups over finite fields, local fields or power series fields.
- A type building is a set of chambers, all pairwise adjacent.
- Buildings of type are in bijection with generalised -gons (see [Batten] and [Ronan, Proposition 3.2]). There is no known classification, even for , where they are in bijection with combinatorial projective planes. The known examples are given in [Batten].
- The buildings of type are trees such that every vertex has valency ≥ 2.
- There is a "free construction" of rank 3 affine buildings given by Ronan [R2] where the building is built outwards from a chamber by gluing together rank 2 spherical buildings. The freedom in the choices of the spherical buildings in this construction illustrates that a classification of rank 3 affine buildings in the spirit of the rank ≥ 4 classification is impossible.
For , a generalised m-gon is a connected graph satisfying
- the vertices of can be partitioned into "type 1" and "type 2" such that no two vertices of the same type are connected by an edge,
- the maximum distance between two vertices of is ,
- the length of the shortest circuit in is .
A combinatorial projective plane consists of a set of lines , a set of points , and an incidence relation between points and lines (a subset of ; write if is incident to ) such that
- If then there exists a unique such that and ,
- If then there exists a unique such that and ,
- There exist such that there is no containing three of .
Notes and References
This page is the result of joint work with James Parkison in 2006. A significant part of this page overlaps with a file buildings12-18-06.tex in Work2007/Bites2007.
References
[Br] K. Brown, Buildings, Springer-Verlag, New York, 2002. ISBN: ?????? MR??????.
[Ro] M. Ronan, Lectures on Buildings, Perspectives on Mathematics, Academic Press, 1989 ISBN: ?????? MR??????.
[Ti] J. Tits, Buildings of Spherical Type and Finite BN-pairs, Lecture Notes in Mathematics, Springer-Verlag, volume 386, 1974. ISBN: ?????? MR??????.